This article was last updated on <span id="expire-date"></span> days ago, the information described in the article may be outdated.
之前我们介绍了几种初等积分法求解微分方程(实际上是之后),事实上这些方法能够处理的微分方程数量是很有限的;那么对于无法求得解析解的微分方程,我们希望能够得知其近似解,并且确定解是否存在以及解的个数。
这一节我们介绍的重要的 Picard 存在唯一性定理就给出了 Cathy 问题存在唯一解的充分不必要条件。
定理的主要证明思路来自:
- Bilibili 王飞老师 的 ODE 课程(这个老师讲的真的很棒)
- 丁同仁教授的 《常微分方程教程》
- WikiPedia 上的一些补充
下面我们就开始吧!
Lipschitz 条件
定义函数 $f(x, y)$ 在区域 $D$ 上满足 Lipschitz 条件:
$$
\newcommand\d[1]{\text{d}#1}
|f(x, y_1) - f(x, y_2)| \leq L |y_1 - y_2|
$$
其中常数 $L > 0$,则称函数 $f(x, y)$ 在区域 $D$ 上满足 Lipschitz 条件
可以得到,如果函数 $f(x, y)$ 在凸形区域 $D$ 内对 $y$ 有连续的偏导数,则 $f(x, y)$ 在 $D$ 内对 $y$ 满足 Lipschitz 条件,反之则不一定成立,例如:
$$
f(x, y) = |y|
$$
对 $y$ 满足 Lipschitz 条件,但是当 $y = 0$ 时该函数对 $y$ 没有微商
关于凸形区域概念的补充
在某个区域 $D$ 内任取两个点 $(x_0, y_0), (x_1, y_1)$,如果他们的构成的直线段的任意部分都在该区域内,那么称该区域为一个凸区域。实际上,可以通过计算得到这个直线段的方程:
$$
\frac{x - x_0}{x_1 - x_0} = \frac{y - y_0}{y_1 - y_0} ,;(x_0 \leq x \leq x_1, y_0 \leq y \leq y_1)
$$
直观的来说就是该区域的边界弯曲方向是一致的偏微分和偏导数(偏微商)
微分和导数在单元函数的概念中就有区别:
微分指的是某个函数在某个方向上的一个微小变化量;注意这里指的是函数值的微小变化量,使用自变量的一个微小变化量代表,实际上是一个线性函数
导数指的是函数在某一自变量方向上微小的函数值变化量与自变量变化量的比值,从这个概念上可以得到微分实际是导数与微小变化量的乘积,以二元函数 $z = F(x, y)$ 举例:
$$
\d{z} = \frac{\partial{F(x, y)}}{\partial{x}} \d{x} + \frac{\partial{F(x, y)}}{\partial{y}} \d{y}
$$
例题
若存在一个函数 $f(x, y)$,其对于 $y$ 的偏导数 $f_y(x,y)$ 在区域 $R$ 上有界,试证明函数在区域 $R$ 上满足 Lipschitz 条件。
根据题目条件:
$$
\exists L > 0 , \forall (x, y_0) \in R \rightarrow f_y(x,y_0) < L
$$
那么根据拉格朗日中值定理,在任意的两个 $(x, y_1), (x, y_2) \in R$ 之间存在一个点 $(x, \xi)$,使得:
$$
|f(x, y_1) - f(x, y_2)| < |f(x, \xi)(y_1 - y_2)| \leq L|y_1 - y_2|
$$
则函数在区间 $R$ 上满足 Lipschitz 条件
由此可以得到,如果一个函数满足导数在区间内有界,那么它一定满足 Lipschitz 条件
满足 Lipschitz 条件的函数我们称它在区间上 Lipschitz 连续
连续、一致连续、Lipschitz 连续
函数 $f(x)$ 在区间 $(a, b)$ 上连续:
$$
\forall x_0 \in (a, b) ,; \forall \epsilon > 0 ,; \exists \delta(\epsilon, x_0) ,; |x - x_0| < \delta \rightarrow |f(x) - f(x_0)| < \epsilon
$$
函数 $f(x)$ 在区间 $(a, b)$ 上一致连续:
$$
\forall x_1, x_2 \in (a, b) ,; \forall \epsilon > 0 ,; \exists \delta(\epsilon) ,; |x_1 - x_2| < \delta \rightarrow |f(x_1) - f(x_2)| < \epsilon
$$
Lipschitz 连续:
$$
\forall x_1, x_2 \in (a, b) ,; \forall \epsilon > 0 ,; \exists \delta = \frac{\epsilon}{L} \rightarrow |f(x_1) - f(x_2)| < \epsilon
$$
这三者条件逐渐变强,因此有:导数有界 > Lipschitz 条件 > 一直连续 > 连续
但注意,函数可导性与 Lipschitz 并无直接关系,不能相互推出
Picard 存在唯一性定理
设某一个 Cathy 问题:
$$
(E): \frac{\d{y}}{\d{x}} = f(x, y), y(x_0) = y_0
$$
其中 $f(x, y)$ 在矩形区域
$$
R: |x - x_0| \leq a, |y - y_0| \leq b
$$
内 连续,并且对变量 $y$ 满足 Lipschitz 条件, 则 $(E)$ 在区间 $I = |x_0 - h, x_0 + h|$ 上又且仅有一个解 $y = \phi(x)$,其中:
$$
h = \min { a, \frac{b}{M} }, M > \max\limits_{(x, y) \in R} |f(x, y)|
$$
思路
首先分析 $h$ 的取值范围中必须要有 $a$ 是因为 $f(x, y)$ 是一个限定在矩形区域 $R$ 上的函数,而 $x$ 的范围由 $a$ 确定
而在闭区间上连续的函数 $f(x, y)$ 根据连续函数的有界性定理必定存在一个 $M$ 使得:
$$
M > \max\limits_{(x, y) \in R} |f(x, y)|
$$
之后我们采取如下步骤:
将微分方程转化成一个积分方程,并构造一个序列(Picard 序列)
$$
\phi_{n + 1}(x) = y_0 + \int_{x_0}^{x} f(t, \phi_n(t)) \d{t} ,;(x\in I) ,; (n = 0, 1, 2, \cdots) ; \wedge ; \phi_0(x) = y_0
$$用数学归纳法保证构造的序列有意义,即:$|\phi_n(t) - y_0| \leq b, n = 0, 1, 2\cdots$
对两侧的 $n$ 同时取极限,保证 $\phi_n(x)$ 一致收敛到 $\phi(x)$,使得极限号能够穿过积分运算
关于点态收敛与一致收敛
首先我们来看点态收敛:设 ${ f_n }$ 是一组在 $D$ 上“收敛”的函数序列,如果:
$$
\forall x_0 \in D, \forall \epsilon > 0, \exists N, \forall n > N, |f_n(x_0) - f(x_0)| < \epsilon
$$
那么这种收敛被称为点态收敛,再来看一致收敛:
$$
\forall \epsilon > 0, \exists N, \forall n > N, \forall x \in D, |f_n(x) - f(x)| < \epsilon
$$
可以看到,在点态收敛中,$N$ 的取值与 $x_0$ 有关;而在一致收敛中,$N$ 的取值仅与 $\epsilon$ 有关。这就是点态收敛与一致收敛最本质的区别。换句话说,点态收敛要求在某一点上满足这个条件 —— 其根本是首先找到一个点,之后找到满足这个条件的 $N$,之后将所有满足该条件的点聚合起来称为一个收敛域;而一致收敛是找到一个 $N$,之后找到满足这个条件的所有 $x$,称为收敛域。
从几何上来说:
点态收敛要求函数列在收敛域上某个点的 $\epsilon$ 临域内都无限趋近收敛函数 $f(x)$
一致收敛要求函数列在收敛域上全部的图像都落在带状区域:
$$
{ (x, y) | x \in D, S(x) - \epsilon < y < S(x) + \epsilon }
$$
通过这样的方式,一致收敛就能保证函数序列的连续性;相对应的点态收敛则不能保证。
证明一致收敛的函数 $\phi(x)$ 就是积分方程的解(存在性)
证明这个解是唯一的解(唯一性)—— 任取一个积分方程的解 $\Phi(x)$ 并证明 $\Phi(x) - \phi_n(x) \to 0 \text{ as } n \to \infty$
证明
Cathy 问题 $(E)$ 等价于积分方程:
$$
y(x) = y_0 + \int_{x_0}^{x} f(t, y(t)) \d{t}
$$
事实上,假设原方程的解为 $y = y(x)$,那么:
$$
y’(x) = f(x, y(x)) (x \in I) ; \wedge ; y(x_0) = y_0
$$
对上面的等式两侧在区间 $x_0, x$ 上进行积分:
$$
\int_{x_0}^{x} \d{y} = \int_{x_0}^{x} f(x, y(x)) \d{x} \Rightarrow y(x) = y(x_0) + \int_{x_0}^{x} f(t, y(t)) \d{t}
$$
积分区间选取 $x_0, x$ 是因为解是一个关于 $y = y(x)$ 的显函数,确定 $x$ 区间后可以将 $f(x, y)$ 限制在区域 $I$ 内反过来,假设 $y = y(x)$ 是积分方程的解,那么:
$$
y(x) = y_0 + \int_{x_0}^x f(t, y(t)) \d{t} \Rightarrow y’(x) = f(x, y(x))
$$
因此, Cathy 问题 $(E)$ 解的存在及唯一性等价于积分方程在区间 $I$ 上有且仅有一个解构造一个函数序列:
$$
\phi_{n + 1}(x) = y_0 + \int_{x_0}^{x} f(t, \phi_n(t)) \d{t} ,;(x\in I) ,; (n = 0, 1, 2, \cdots) ;\wedge ; \phi_0(x) = y_0
$$
关注命题 $|\phi_n(x) - y_0| \leq b ,, (n = 0, 1, 2, \cdots)$当 $n = 0$ 时:$|\phi_0(x) - y_0| = 0 \leq b$ 成立
假设 $n = k$ 时: $|\phi_k(x) - y_0| \leq b$ 成立
当 $n = k + 1$ 时:
$$
|\phi_{k+1}(x) - y_0| \leq \int_{x_0}^{x} |f(t, \phi_k(t))| \d{t}
$$
因为函数 $f(t, \phi_k(t))$ 在区域 $R$ 上连续,那么根据闭区间的有界性定理,函数有界,既存在 $M > 0$,使得:
$$
\int_{x_0}^{x} f(t, \phi_k(t)) \leq M|x - x_0|
$$
而根据定理条件,$|x - x_0| \leq h \leq \frac{b}{M}$,代入上式:
$$
\int_{x_0}^{x} f(t, \phi_k(t)) \leq M|x - x_0| \leq Mh \leq b
$$那么根据数学归纳法能够得到:
$$
\forall n , |\phi_n(x) - y_0| \leq b
$$
下来证明 $\phi_n(x)$ 一致收敛到 $\phi(x)$ 上,使用级数:
$$
\phi_n(x) = \sum_{k = 1}^{n} |\phi_k(x) - \phi_{k - 1}(x)| + \phi_0(x)
$$
对于第一项 $|\phi_1(x) - \phi_0(x)|$,$\phi_0(x) = y_0$
$$
|\phi_1(x) - \phi_0(x)| \leq \int_{x_0}^{x} |f(t, y_0)| \d{t} \leq M(x - x_0)
$$
对于第二项 $|\phi_2(x) - \phi_1(x)|$
$$
|\phi_2(x) - \phi_1(x)| \leq \int_{x_0}^{x} |f(t, \phi_1(t)) - f(t, y_0)| \d{t}
$$
使用定理中的 Lipschitz 条件:$|f(t, \phi_1(t)) - f(t, y_0)| \leq L|\phi_1(t) - y_0|$:
$$
\int_{x_0}^{x} |f(t, \phi_1(t)) - f(t, y_0)| \d{t} \leq L \int_{x_0}^{x} |\phi_1(t) - y_0| \d{t} = L \int_{x_0}^{x} |\phi_1(t) - \phi_0(t)| \d{t} \leq LM \int_{x_0}^{x} (t - x_0) \d{t} \
\leq \frac{1}{2}ML (x - x_0)^2
$$
对于第三项 $|\phi_3(x) - \phi_2(x)|$ 同理可得
$$
|\phi_3(x) - \phi_2(x)| \leq L \int_{x_0}^{x} |\phi_2(t) - \phi_1(t)| \d{t} \leq \frac{1}{2} M L^2 \int_{x_0}^{x} (t - x_0)^2 \d{t} \
= \frac{ML^2}{3!} (x - x_0)^3
$$
以此类推 可以得到:
$$
|\phi_n(x) - \phi_{n - 1}(x)| \leq \frac{M}{L} \cdot \frac{L^n (x - x_0)^n}{n!} \leq \frac{M}{L} \cdot \frac{(Lh)^n}{n!}
$$
对不等式右侧的数项级数进行判别:
$$
\sum_{n = 1}^{\infty} \frac{M}{L} \frac{(Lh)^n}{n!} = \frac{M}{L} \left( \sum_{n = 0}^{\infty} \frac{(Lh)^n}{n!} - 1 \right) = \frac{M}{L} (e^{Lh} - 1)
$$
收敛,那么级数 $\phi_n(x)$ 一致收敛于 $\phi(x)$根据上面的结论:
$$
\lim_{n \to \infty} \phi_{n + 1}(x) = y_0 + \lim_{n \to \infty} \int_{x_0}^{x} f(t, \phi_n(t)) \d{t} \
f(t, \phi_n(t)) \rightrightarrows f(t, \phi(t)) \
\Rightarrow \phi(x) = y_0 + \int_{x_0}^{x} f(t, \phi(t)) \d{t}
$$
所以 $\phi(x)$ 为积分方程的解任取一个微分方程的解 $\Phi(x)$,那么与上面的级数证明方法类似有:
$$
\Phi(x) = y_0 + \int_{x_0}^{x} f(t, \Phi(t)) \d{t}\
|\Phi(x) - \phi_{0}(x)| \leq \int_{x_0}^{x} |f(t, \Phi(t)) - \Phi(t)| \d{t} \leq M(x - x_0) \
|\Phi(x) - \phi_{1}(x)| \leq … \leq \frac{ML}{2}(x - x_0)^2 \
|\Phi(x) - \phi_{n}(x)| \leq … \leq \frac{(Lh)^{n + 1}}{(n + 1)!} \to 0
$$
可以得到 $\phi_n(x)$ 一致收敛到 $\Phi(x)$所以 $\phi(x)$ 是原积分方程的唯一解
注意
Picard 定理又称为 存在唯一性定理,分析以下几个问题:
假设函数 $f$ 在 $R$ 上的最大值 $M$ 较小,满足:
$$
a \leq \frac{b}{M} \Rightarrow M \leq \frac{b}{a} \Rightarrow h = a
$$
而根据定义函数 $f = \frac{\d{y}}{\d{x}}$ 即反映了解在区间上的导数(也就是斜率)比较小而如果最大值 $M$ 比较大,使得:
$$
h = \frac{b}{M}
$$
那么解在区间内的斜率就比较大实际上,满足 Lipschitz 连续的函数,存在一个双圆锥(图中为白色)其顶点可以沿着曲线平移,使得曲线总是完全在这两个圆锥外:
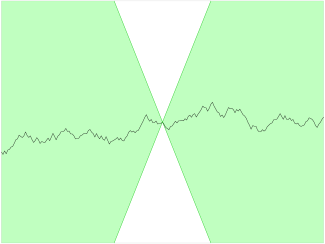
函数连续 + Lipschitz 能够推出 存在唯一,但这是一个 充分不必要条件
这也就意味着,函数 $f$ 有可能是不连续的但是其解可能是存在唯一的;同样的,Lipschitz 条件也无法推出解的存在唯一性
当给定的矩形区域条件 $|y - y_0| \leq b \to \infty$ 时,$f(x, y)$ 在带状区域 $R: {(x, y) | x \in [\alpha, \beta]}$ 连续切满足 Lipschitz 条件,那么解 $y = \phi(x)$ 在区间 $[\alpha, \beta]$ 有定义
隐函数微分方程的存在唯一性
假设给定的微分方程有如下形式:
$$
F(x, y, y’) = 0 \wedge
y(x_0) = y_0, y’(x_0) = y_0’
$$
如果给定的隐函数可以显化,则可以使用上面得到的 Picard 存在唯一性定理
隐函数存在性定理
如果函数 $F(x, y)$ 满足:
- $F(x_0, y_0) = 0$
- $F(x, y)$ 在点 $(x_0, y_0)$ 的某一个邻域内有连续偏导数
- $F’(x_0, y_0) \neq 0$
那么方程 $F(x, y) = 0$ 在 $(x_0, y_0)$ 的某个邻域内存在一个唯一的函数 $y = f(x)$ 满足 $F(x, y(x)) = 0, y_0 = y(x_0)$,并且有:
$$
\frac{\d{y}}{\d{x}} = - \frac{\partial{F(x, y)}}{\partial{x}} \cdot \frac{\partial{y}}{\partial{F(x, y)}}
$$
而根据隐函数定理,在某一个邻域内的连续偏导数肯定是有界的,则 Lipschitz 条件被保证,所以只要保证隐函数存在定理就可以保证存在唯一解,综上所述,我们能够得到:
如果在 $(x_0, y_0, y’_0)$ 的某一个邻域中
- $F(x, y, y’)$ 对 $x, y, y’$ 分别都存在连续偏导数
- $F(x_0, y_0, y’_0) = 0$
- $\frac{\partial F(x_0, y_0, y’_0)}{\partial{y’}} \neq 0$
则问题存在唯一解
解的估计与误差
对于满足 Lipschitz 条件的微分方程,我们可以使用 Picard 序列对解进行估计,例如:
$$
\frac{\d{y}}{\d{x}} = y \wedge y(0) = 1
$$
我们逐项分析 Picard 序列:
$$
\phi_0(x) = 1, \phi_1(x) = y_0 + \int_{x_0}^{x} f(t, \phi_0(t)) \d{t} = 1 + \int_{0}^{x} (1 + t) \d{t} = 1 + x + \frac{x^2}{2!} \cdots \
\phi_n(x) = 1 + x + \frac{x^2}{2!} + \cdots + \frac{x^n}{n!}
$$
显然结果是 $e^x$ 的泰勒级数
对于某些很难求解的微分方程,我们可以使用 Picard 序列对解写出级数形式进行逼近;而根据上面对解的唯一性的推导(证明的第五部分):
$$
|\phi_n(x) - \Phi(x)| \leq \frac{M}{L} \cdot \frac{(Lh)^{n + 1}}{(n + 1)!}
$$
我们可以对求得的解进行误差估计,或者求出指定精度的近似解,例如:
$$
\frac{\d{y}}{\d{x}} = x^2 + y^2 \wedge y(0) = 0
\
D = {(x, y) | |x| \leq 1, |y| \leq 1 } \Rightarrow a = b = 1 \
\frac{\partial{f}}{\partial{y}} = 2y \Rightarrow L = 2, M = \max_\limits{(x, y) \in D} = 1^2 + 1^2 = 2 \Rightarrow h = \min { a, \frac{b}{M} } = \frac{1}{2}
$$
如果我们要求解的误差不超过 5%
$$
|\phi_n(x) - \Phi(x)| \leq \frac{M}{L} \cdot \frac{(Lh)^{n + 1}}{(n + 1)!} = \frac{1}{(n + 1)!} \leq 0.05 \Rightarrow n = 3 \
\phi_0(x) = 0 \
\phi_1(x) = \int_{0}^{x} (t^2 + 0) \d{t} = \frac{1}{3} x^3 \
\phi_2(x) = \int_{0}^{x} (t^2 + \frac{1}{9} t^6) \d{t} = \frac{1}{3} x^3 + \frac{1}{56} x^7 \
\phi_3(x) = \int_{0}^{x} (t^2 + \frac{1}{9} t^6 + \frac{1}{168}t^{10} + \frac{1}{3136} t^{14}) \d{t} = \frac{1}{3} x^3 + \frac{1}{56} x^7 + \frac{1}{1848} x^{11} + \frac{1}{47040} x^{15}
$$
我们观察到,我们给定的定义域在 $[-1, 1]$ 上,而解却落在了 $[-\frac{1}{2} , \frac{1}{2}]$ 上;而如果我们给定的区间拓宽至 $[-2, 2]$ 上,那么:
$$
h = \min { 2, \frac{2}{2^2 + 2^2} } = \frac{1}{4}
$$
而根据函数定理,在某一个邻域内的连续偏导数肯定是有界的,则 Lipschitz 条件被保证,所以只要保证隐函数存在定理就可以保证存在唯一解。
可以看到,给定的连续定义域越大,解的域反而越小,这说明我们的解区间给的太小了。
下一节我们会对使用 Picard 序列求得近似解的误差进行估计,并探讨解的存在区间,借此引出解的延拓概念。

Comments