一个圆形内接三角形是锐角三角形的概率

这是一道之前在b站看视频的时候刷到的美国初中竞赛题，那个up最后给出了一个错误答案，导致我把这道题做了一遍，题并不复杂，但是初中生能用的解题思路我还是没想出来，所以就用了微积分来解题。

首先，由于圆的内街三角形是在圆上任意取得三个点，我们需要按步骤确定每一个点对最终概率的影响。并且，显而易见，由于圆的大小并不影响这个概率，所以我们取一个半径为1的单位元方便运算。对于第一个点$P1$，显而易见不管这个点在哪里，对最终的三角形形状是没有任何影响的，那我们就如图1所示取一个方便观察的位置。

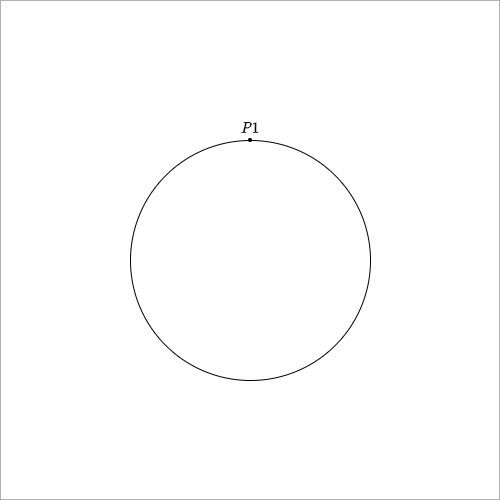
然后我们就需要考虑$P2$对三角形的影响了，首先我们把圆的边进行微分，然后把$P2$的位置看成是任意一个微分出来的小边$\Delta l$中的一个点，如图2。

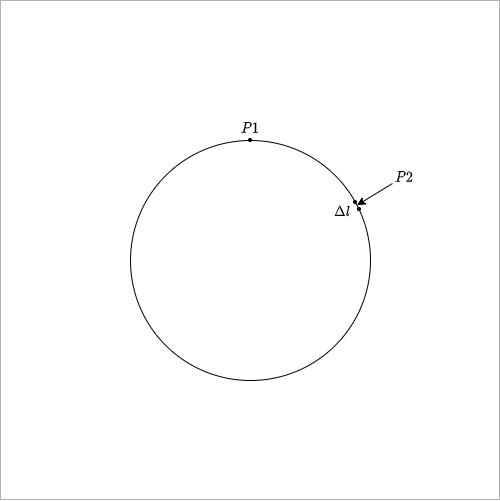
我们可以得出，$P2$在圆任意位置的概率就等于当小边长度$\Delta l$趋近于无穷小的时候小边和圆周长之比:$$\lim_{\Delta l \to 0}\frac{\Delta l}{2\pi}=\frac{dl}{2\pi}$$接下来，我们就需要分析在$P2$固定的情况下，$P3$需要放在哪些地方才能使这三个点形成的三角形为锐角三角形了。

首先，我们如图3所示做几条辅助线。$P1P2Q2Q1$为一个圆的内接矩形，观察这个矩形我们可以看出当$P3$坐落于$Q1$和$Q2$时，$\triangle P1P2P3$是一个直角三角形。而当$P3$是优弧$Q1P1Q2$上的点时，$\triangle P1P2P3$为一个钝角三角形。由此可得，当且仅当$P3$是红线所标的劣弧$Q1Q2$(不包含端点)上的点时，$\triangle P1P2P3$为一个锐角三角形。

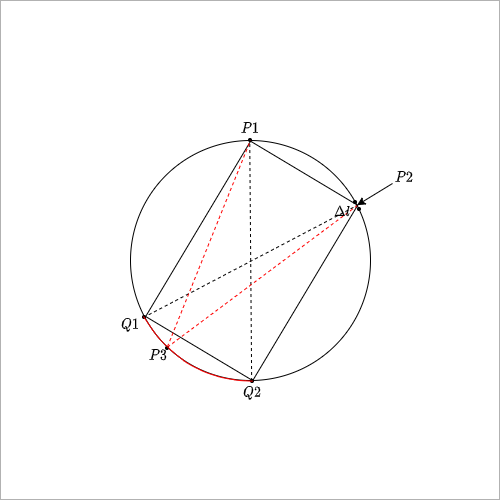
现在三个点的位置都已经分析清楚了，我们只需要对其进行运算就可以了。由余弦定理我们可以得到劣弧$Q1Q2$和劣弧$P1P2$是等长的，并且这个弧的长度与$P2$的位置相关，且可以看作是无数微分出的小边$\Delta l$从$P1$为起点累加所得，因此这个长度我们直接设置为$l$。因此在确定了$P2$的情况下(也就是确定了$l$)，$P3$使得$\triangle P1P2P3$为锐角三角形的概率为$Q1Q2$的弧长比上圆的周长即$\frac{l}{2\pi}$。

现在就差最后一步进行积分了，但是我们要注意$P2$这个点一但从$P1$顺时针旋转到圆的另一半时，弧$Q1Q2$的长度就不等于$l$了。如图4所示，当$P2$移动到圆的左半边时，$P1P1$从劣弧变为了优弧(红线所标)，其长度$l$不再是劣弧$Q1Q2$的长度，所以我们进行积分时只能取右半边做积分，但是圆左右部分是对称的，所以左半部分的概率可以看成是$P2$从$P1$逆时针旋转所得，所以$P2$不论在左边还是右边最后的概率是相同的，并且$P2$在左半部分的概率与在右半部分的概率是相等的，假设右半部分积分出的概率为$p$，那么实际的概率就是$\frac{p}{2}$，左边同样是$\frac{p}{2}$，因此总的概率就是$\frac{p}{2}+\frac{p}{2}=p$。也就是说只用对右半部分进行积分就可以得到总的概率了。

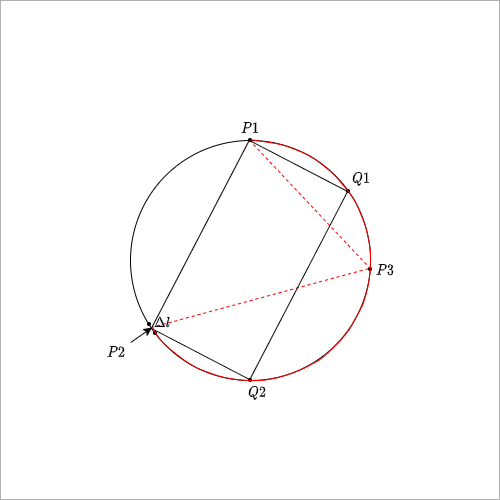
根据之前所得的式子我们直接进行积分得：$$p=\int_0^{\pi}\frac{dl}{\pi}\frac{l}{2\pi}=\frac{1}{4}$$

可以注意到这个式子中之前的$\frac{dl}{2\pi}$被换成了$\frac{dl}{\pi}$，这正是因为我们只对右半部分进行积分所进行的改变，其积分上限$\pi$而不是$2\pi$也对应着这个改变。

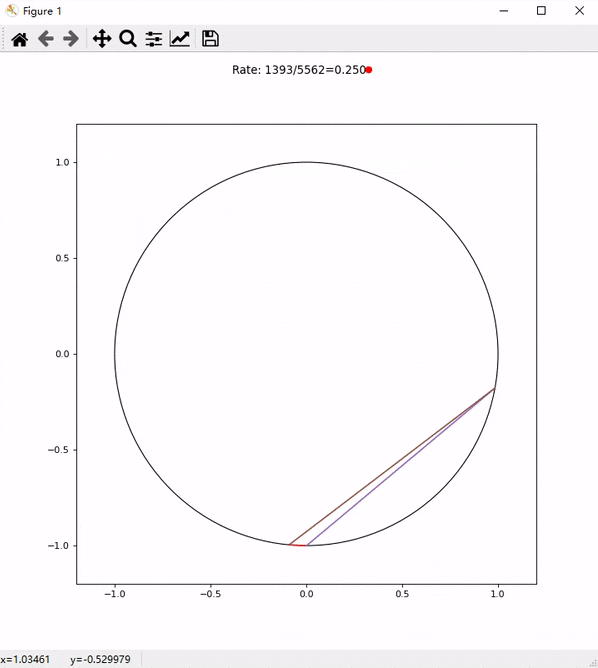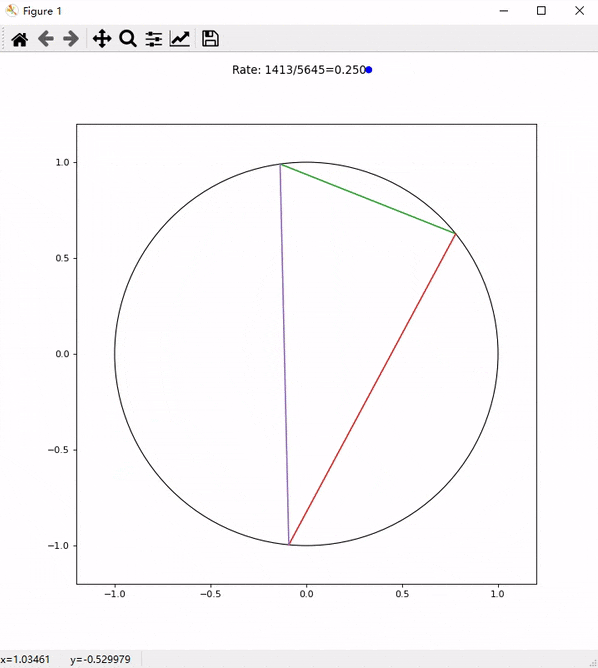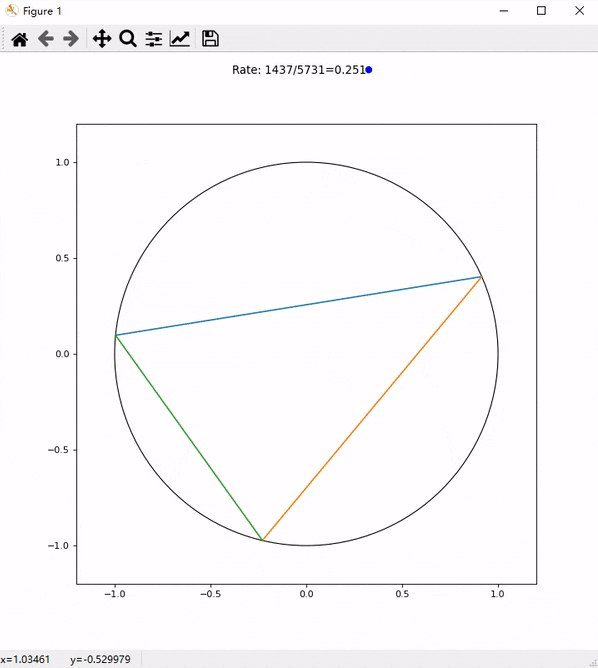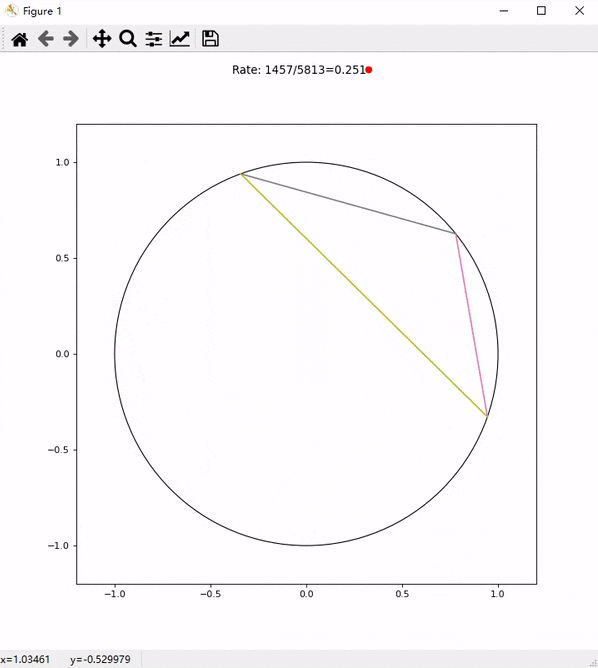
为了验证这个结果，我还专门写了一段代码来检测。如图5所示，程序不断随机在一个园内生成一个内接三角形，并且判断其是否为锐角三角形，如果是上面数字的右边的点会变为蓝色，如果不是就变为红色。Rate后面的数字分别是目前所有随机出的三角形中锐角三角形的个数和总的生成的三角形的个数以及其比例。

我们加快速度，并且截取超过5000次随机过程之后的比例。如图6所示,这个比值不断趋近于0.25与我们的运算结果相符。

附代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

import numpy as np
import time
import matplotlib.pyplot as plt
pi = 3.141592653589793238462643383279502884
 
 
def create_circle():
    circle = []
    for i in range(0, 3):
        angle = np.random.uniform(0, 2 * pi, [1])
        point = np.zeros([2], dtype=float)
        point[0] = np.cos(angle[0])
        point[1] = np.sin(angle[0])
        circle.append(point)
    return circle
 
 
def is_acute(circle):
    for i in range(0, 3):
        vec1 = circle[(i + 1) % 3] - circle[i]
        vec2 = circle[(i + 2) % 3] - circle[i]
        if np.dot(vec1, vec2) <= 0:
            return False
    return True
 
 
fig = plt.figure(figsize=(9, 9), dpi=80)
a = fig.add_subplot()
plt.axis('scaled')
plt.ion()
plt.show()
a.add_artist(plt.Circle((0, 0), radius=1, fill=False))
n = 0
x = 10000
t = plt.text(0.3, 1.4694, "●")
for i in range(1, x+1):
    circle = create_circle()
    tri = []
    for k in range(0, 3):
        ln, = a.plot([circle[k][0], circle[(k+1) % 3][0]], [circle[k][1], circle[(k+1) % 3][1]])
        tri.append(ln)
    plt.axis([-1.2, 1.2, -1.2, 1.2])
    supt = "Rate: "
    if is_acute(circle):
        n += 1
        t.set_c('blue')
    else:
        t.set_c('red')
    supt += (str(n) + "/" + str(i) + "=" + format(n/i, '.3f'))
    plt.suptitle(supt)
    plt.pause(0.01)
    for lise in tri:
        lise.remove()
print(n/x)