图论 - 最小生成树与 Kruskal 算法

这篇文章我们来讨论最小生成树以及一个生成最小生成树的算法 - Kruskal 算法。

最小生成树

树与生成树

首先我们要知道什么是树：

任意两个顶点间只存在唯一一条路径的图被称为树。

之后我们要知道什么是生成树：

无向图 $G$ 的生成树是具有 $G$ 的全部顶点，但边最少的连通子图。

之前我们介绍过连通性的概念：对于图 $G(V, E)$ 来说，选取顶点集合的两个不同顶点形成的偶对 $(v_a, v_b)$，若在该图中同时存在一条路径能过连接这两个顶点，那么称这两个顶点具有连通性。

同样的，$\forall v_i, v_j \in V$ 如果 $v_i, v_j$ 都具有连通性，那么称这个图是一个连通图。简单的说，就是没有孤立点的图被称为连通图；那么类似的，连通子图就是某个图的连通分量。

有了这个概念，我们就可以考虑这个“最小”的定义；很容易的，我们就能够想到这个最小应该是定义在路径的长度之上，因为只有在一个图中只有权值能够形成偏序关系：

最小生成树其实是 最小权重生成树 的简称。

给出它的正式定义：

在一个无向图 $G = (V, E)$ 中使用函数 $w(u, v)$ 计算相邻节点间边的权重，如果存在 $T \subset E$，使得图 $(V, T)$ 为树，并且满足：
$$
w(T) = \sum_{(u, v) \in T} w(u, v)
$$
最小，那么称图 $(V, T)$ 为 $G$ 的最小生成树。

特殊性质

下来思考一个树的特殊性质；我们都知道对于一个顶点数为 $v$ 的图来说，其最大的边数量可能为 $v(v-1)$，但是这个值是不确定的；而对于顶点数为 $v$ 的树来说，由于任意两个顶点之间只存在唯一一条路径，那么这棵树的边数量是确定的：
$$
|E| = v - 1
$$
并且根据树的定义，如果在某一个图中存在环 - 也就是从某个顶点到另外一个顶点不只存在一条路径，那么这个图不能够被称为树，所以我们又得到了一个很有用的性质：

树中不存在环。

接下来我们思考一个连通图可能有多少个最小生成树。事实上，最小生成树的数量与边函数的值有关：

如果图的每一条边权值都不相同，那么最小生成树将只有一个。

证明过程这里不表，贴下相关内容的链接：

最小生成树 - 维基百科

（其实我也是看 Wikipedia 上的嘿嘿😁）

有了这些性质，我们就可以很简单的理解 Kruskal 算法了。

Kruskal 算法

这个算法可能是图论中比较直观的算法了 - 至少是我一遍就能看明白的并且理解的算法。它就是利用了上面我们说的树的几个特殊性质来求解最小生成树的，步骤很简单：

0. 首先将图 $G(V, E)$ 的边集合拿出按照权值进行排序
1. 之后从最小权值的边开始不断 “回填”
2. 在回填过程中如果发现形成了环，则跳过这条边的回填
3. 当回填的边数量达到 $v - 1$ 时停止，其中 $v$ 是原图顶点集合的势

下面是 Wikipedia 上一个很直观的 Gif，基本看一遍就能明白了。

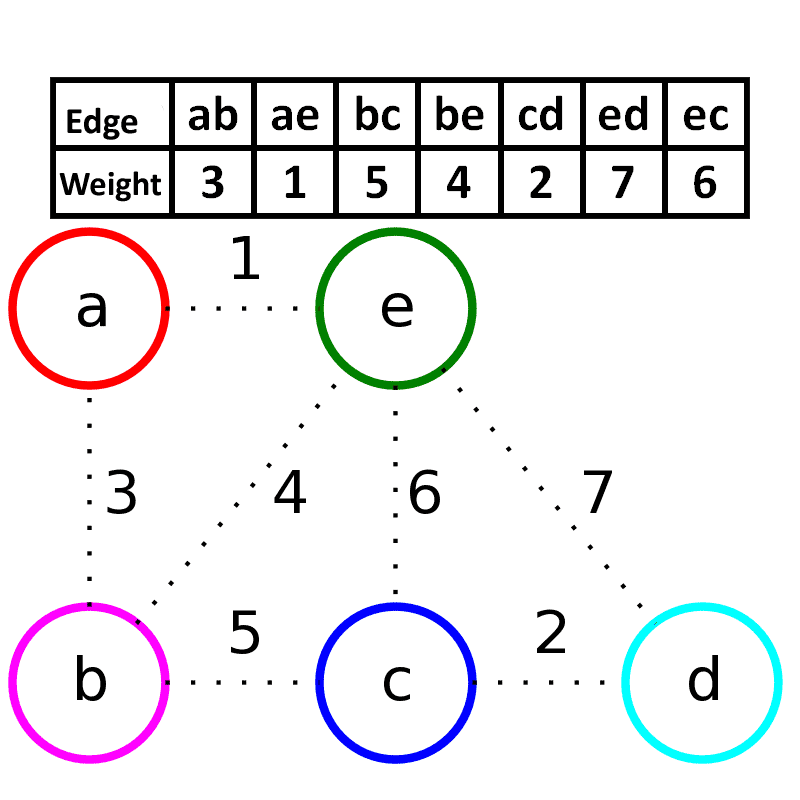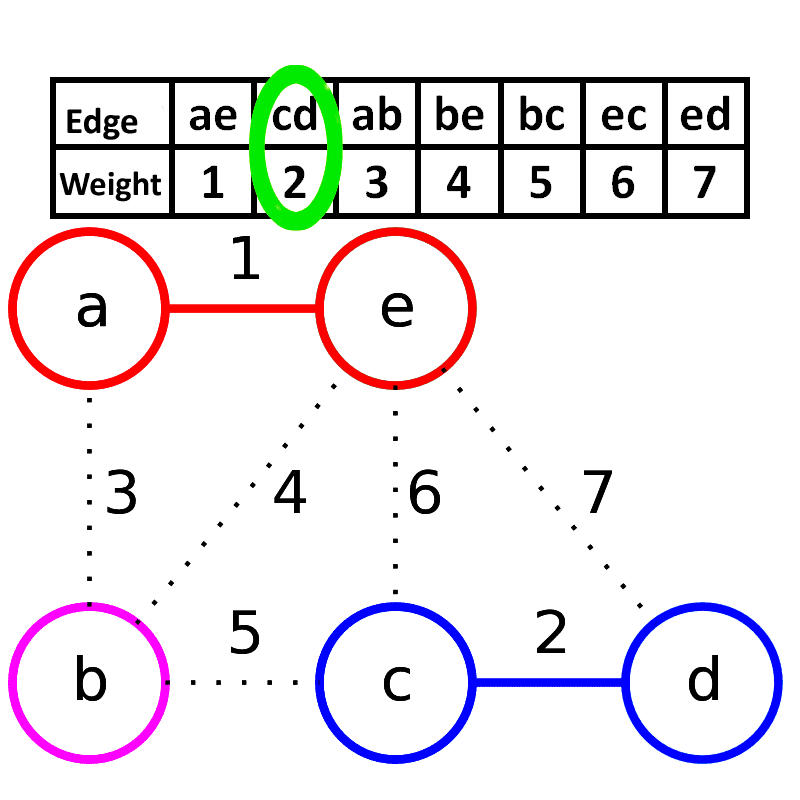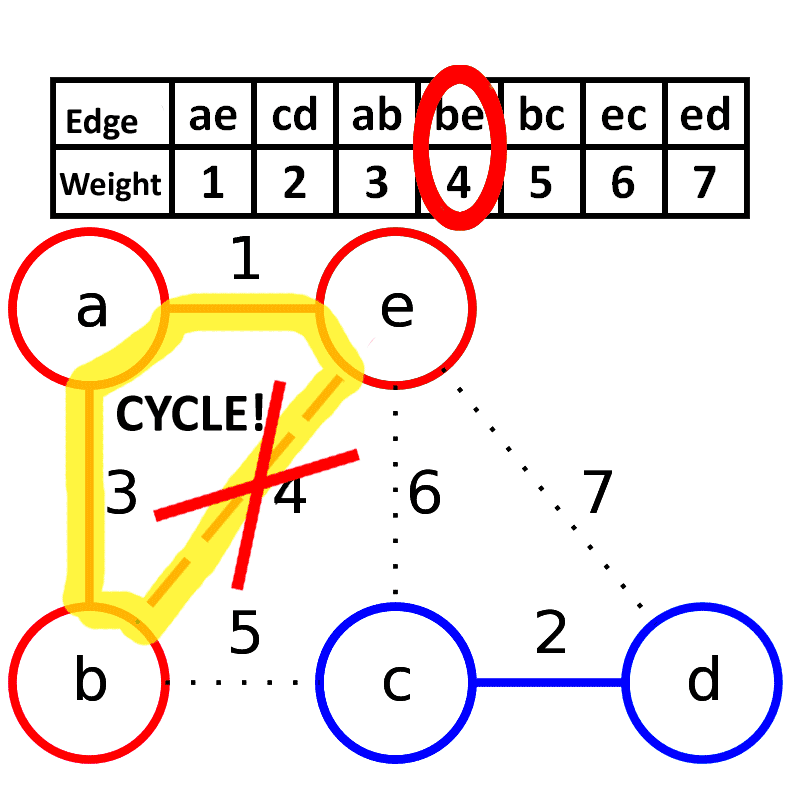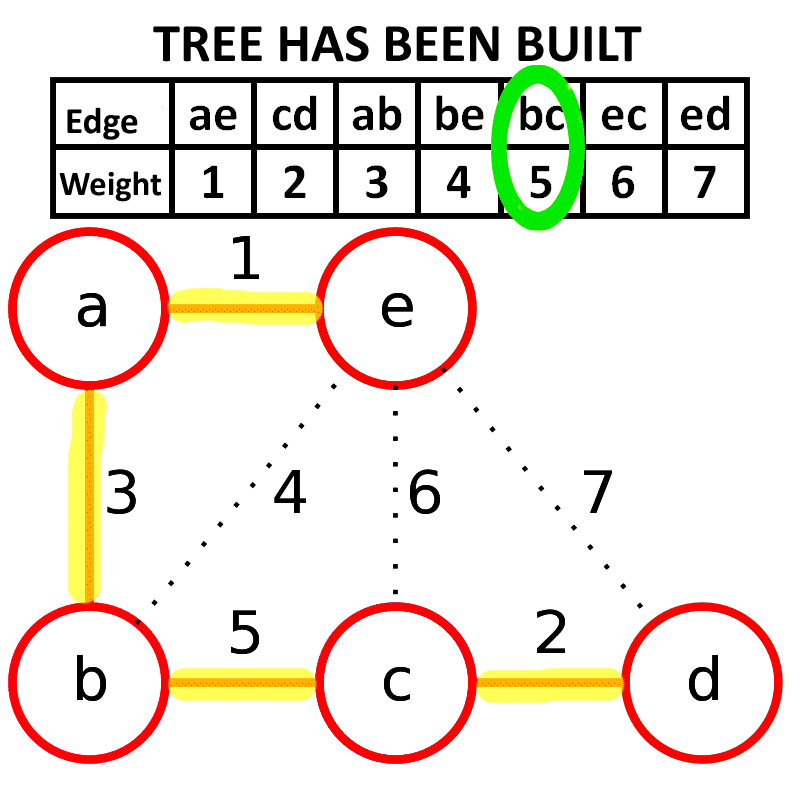
正确性证明

简单是简单，那么为什么这样就能找到最小生成树呢？

首先，我们寻找了 $n-1$ 条边，并且保证这个生成子图中没有环，所以它至少是一个生成树；

其次，回填的过程是按照权值进行的，那么最后“使用”的边的权值和一定是最小的。

回路检测

有朋友可能会有疑问，在上面所述过程的第2步，该怎么检查是否出现环呢？难道要跑一遍DFS/BFS吗？

其实根本不用，用并查集就可以解决，因为这个添加过程是逐步进行的，我们只需要在内存中维护一份“已经添加节点”集合：当每次回填边时，将边的两个顶点添加进这个集合即可。

当下一次添加时，检查一下现在操作的这条边的两个顶点是否都在该集合中即可，当发现都在时意味着出现了环。

关于 Kruskal 算法就介绍这么多。