快速平方根算法 - 从卡马克的魔法数字谈起

This article was last updated on <span id="expire-date"></span> days ago, the information described in the article may be outdated.

大家应该都听说过雷神之锤 3 中那段神奇的快速平方根倒数算法 —— 它因为使用了魔法数字：0x5f3759df 而闻名：

float InvSqrt(float x) {
    float xhalf = 0.5f*x;
    int i = *(int*)&x;
    i = 0x5f3759df - (i >> 1);
    x = *(float*)&i;
    x = x*(1.5f - xhalf*x*x);
    return x;
}

事实上，这个算法使用的方法是传统的牛顿迭代法 —— 之所以它能够在常数时间内给出结果，是因为这个魔法数字可以让迭代开始时的值就已经很接近实际根了。

下面我从牛顿迭代开始，一步步实现一个快速平方根算法，并探究这个魔法数字到底是怎么来的。

牛顿迭代

要求一个数 $a$ 的平方根 $x$，实际上求的就是方程 $f(x) = x^2 - a = 0$ 的根；而计算机中求解这类方程数值解最常用的方法就是牛顿迭代，具体方法如下：

首先选择一个接近方程根的点 $x_0$，计算得到 $f(x_0)$ 与 $f’(x_0)$
计算函数在该点处的切线与 $x$ 轴的交点：
$$
(x - x_0) \cdot f’(x_0) + f(x_0) = 0
$$
解出 $x$，并将其记为 $x_1$，这个点通常会比 $x_0$ 更接近方程根，于是可以不断的迭代上面的方法进行逼近
对于给定的精度 $\epsilon$，重复上面的方法，直到：
$$
x_n - x_{n - 1} \leq \epsilon
$$

上面的切线方程其实也可以看做用 Taylor 展开的前两项，线性近似函数并求解：
$$
f(x) = \sum_{n = 0}^{\infty} \frac{ f^{(n)}(x_0) }{n!} (x - x_0)^n = f(x_0) + f’(x_0)(x - x_0) + \dots
$$
下面的动图可以很好的解释这个过程：

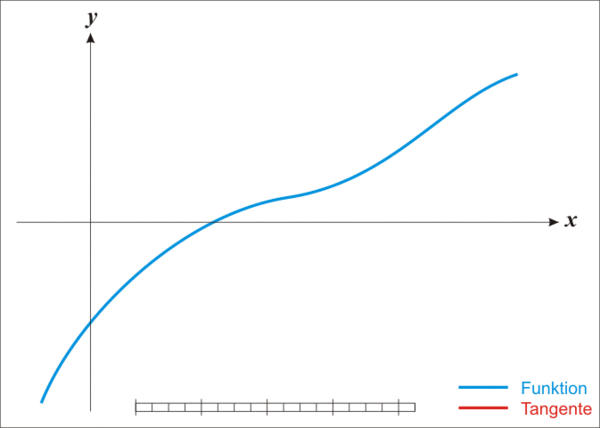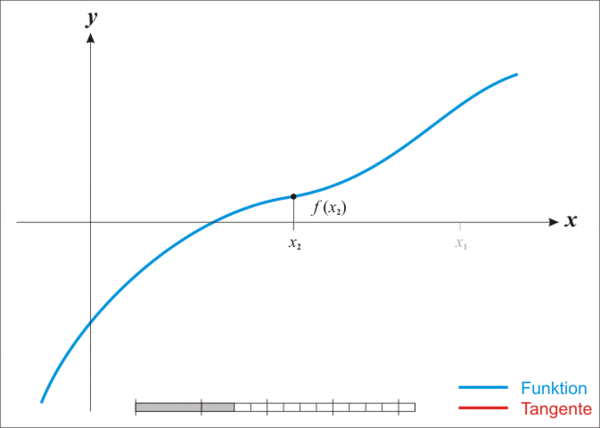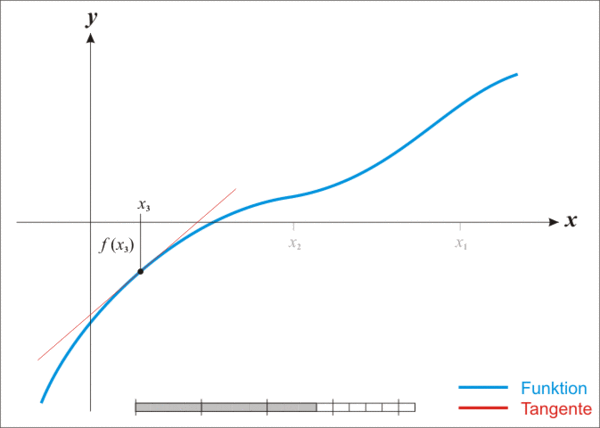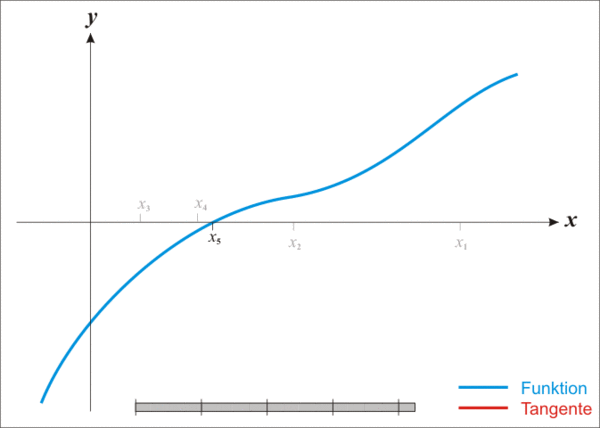
初步实现

假定第一次迭代是从 $x = x_0$ 处开始的，那么：
$$
f’(x_n) = 2x_n \Rightarrow x_{n + 1} = x_n - \frac{f(x_n)}{f’(x_n)} = x_n - \frac{x_n}{2} + \frac{a}{2x_n} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right)
$$
其中 $a$ 是要求平方根的数。

利用上面的方法，已经可以写出一个简单版本的 sqrt 函数了：

#define EPSILON 1e-14

double sqrt(double x) {
    double a = x;
    double guess = 0;
    while (abs(guess - x) > EPSILON) {
        guess = x;
        x = (x + a / x) / 2;
    }
    return x;
}

可以看出，随着 $a$ 的增大，根到 $x_0$ 的距离也越来越远，那么需要迭代的次数也越来越多：

sqrt(1) = 1.000000 - 1 iters
sqrt(10) = 3.162278 - 7 iters
sqrt(100) = 10.000000 - 9 iters
sqrt(1000) = 31.622777 - 11 iters
sqrt(10000) = 100.000000 - 12 iters
sqrt(100000) = 316.227766 - 14 iters
sqrt(1000000) = 1000.000000 - 16 iters
sqrt(10000000) = 3162.277660 - 17 iters
sqrt(100000000) = 10000.000000 - 19 iters

浮点数的内存布局

现代计算机在浮点数的内存布局方面使用的标准为 IEEE 754，其本质是二进制浮点数的科学计数法：

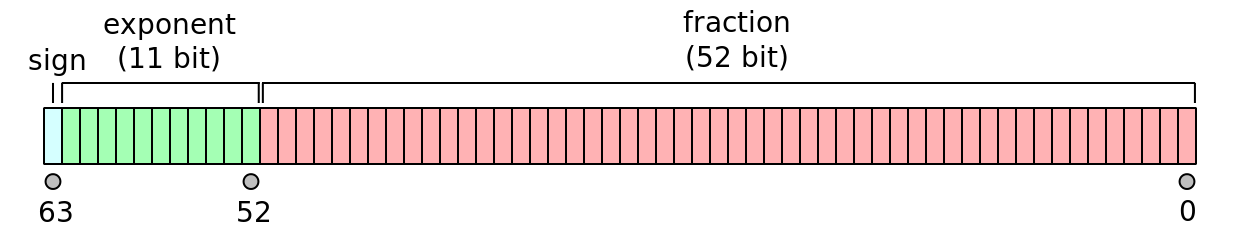
IEEE 754

其中：sign 是符号位，exponent 是指数部分，fraction 是小数部分；为了方便快速比较浮点数指数的大小，需要对实际的指数加 $2^{10} - 1 = 1023$ 进行保存。

例如：
$$
3.125_\text{d} = 2^{0} + 2^{1} + 2^{-3} = 11.001_\text{b} = 1.1001 ^ {1}_{b}
$$

由于小数点前一定为 $1$，所以实际保存的二进制数为（以 double 为例）：
$$
0_{\text{sign}} \ 10000000000_{\text{exp}} \ 100100000000000000000000000000000000000000000000000_{\text{frac}}
$$
这种表示方法给优化上面的算法提供了空间：如果可以先将指数部分直接原来的一半，那么就可以将初次迭代的位置向根方向大大靠近。

第一个魔法数字

有了上面的想法，那么便可以先进行实现：浮点数保存的指数位为实际的指数加 1023，如果要将指数除以 2 的话，可以先将其增加 1023，之后再除以 2：

1 2	exp := real_exp + 1023; (exp + 1023) / 2 = real_exp / 2 + 1023

根据上面 IEEE 754 的 64 位内存布局，指数位上的 1023 对应的二进制为：0x3ff000...

将 double 取地址转为 64 位整形指针，除以 2 则用位移实现：

1 2	unsigned long exponent = (unsigned long )&x; (exponent) = (exponent + 0x3ff0000000000000) >> 1;

这是使用魔法数字 0x3ff0000000000000 优化之后的结果：

sqrt(1) = 1.000000 - 1 iters
sqrt(10) = 3.162278 - 4 iters
sqrt(100) = 10.000000 - 5 iters
sqrt(1000) = 31.622777 - 3 iters
sqrt(10000) = 100.000000 - 5 iters
sqrt(100000) = 316.227766 - 5 iters
sqrt(1000000) = 1000.000000 - 4 iters
sqrt(10000000) = 3162.277660 - 5 iters
sqrt(100000000) = 10000.000000 - 5 iters

可以看到，相比较之前版本的算法，在面对大数字时求解所需的迭代次数减少了很多。

但是，魔法数字还可能带来更多的优化吗？

魔法数字的状态空间

想要得到更多的优化，那么可以对整个魔法数字的状态空间进行一遍搜索，看看相对来说哪一个数字表现更优秀；而之前魔法数字的最后一位为 1，向右位移之后可能覆盖掉小数部分的第一位，所以为了保证搜索的完整性，状态空间的边界应该为：
$$
(\text{0x3fe0000000000000}, \text{0x3fffffffffffffff})
$$
但是整个空间太大了，如果完全存储下来（64 位整型），至少需要 6PB 的空间；想要看出整体的走向，可以先采样之后再分析：

对上面的 C 程序先进行一些修改，以方便使用 matplotlib 绘图：

首先将牛顿迭代的次数改为一次，这样针对性的优化版本可以得到常数的时间复杂度
在函数中动态的使用可以更改的魔法数字
将其编译为可供 ctypes 使用的函数，并使用 numpy 进行包装

之后按照如下方法得到每一个魔法数字对应的误差值：

对指定的魔法数字，在一段空间内随机抽取一部分数字
使用每一个随机抽取的数字，计算一次牛顿牛顿迭代后的值与真实根值的差
对差求得平均值作为该魔法数字的误差值

1
2
3

lib.set_magic(int(magic))
lib.sqrts(self._xs, self._ys)
return numpy.abs(numpy.mean(self._standard - self._ys))

其中 sqrts 是刚刚修改过的求根函数。

这是得到的误差-魔法数函数的大致走势（抽样间隔为 $2^{40}$）：

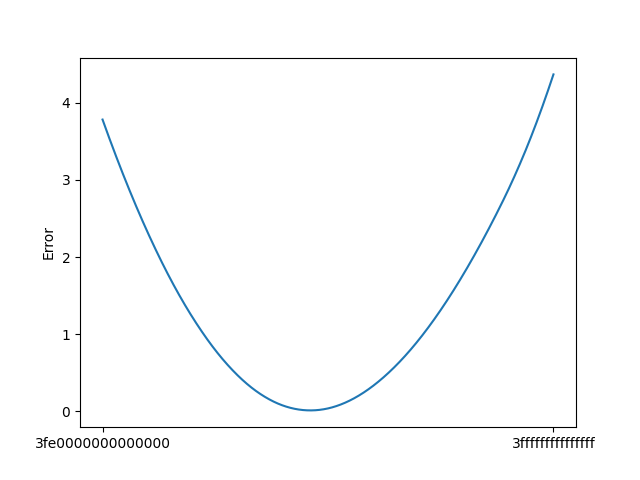
Error

可以看出，存在上个版本其实还有优化空间，一个更好的魔法数字甚至可以将一次牛顿迭代的平均绝对误差降低到很接近 0 的位置。

梯度下降

之前看到网上有用二分法求取魔法数字的；而相对于底部较为平滑的那小段来说，整体上图像的陡峭程度还是较均匀的，所以我决定尝试用梯度下降来求解更好的魔法数字。

要想使用梯度下降，首先得规定这个函数的梯度怎么求取，这里使用了如下方法：

对于每一个给定的魔法数字，按照上面的方法求得左右侧一段范围的一个数对应的误差
如果该数字单侧的距离小于这个范围，那么只使用单侧的误差值
之后使用（右侧误差值 - 左侧误差值）/（2 * 区间长度）定义为该值的导数值
只要区间相对于整体很小，那么这个导数值还是较为准确的

if const.MagicStart + delta < magic and const.MagicEnd - delta > magic:
    return multiply * (self(magic + delta) - self(magic - delta)) / (2 * delta)
if const.MagicStart + delta > magic and const.MagicEnd - delta > magic:
    return multiply * (self(magic + delta) - self(magic)) / delta
if const.MagicStart + delta < magic and const.MagicEnd - delta < magic:
    return multiply * (self(magic) - self(magic - delta)) / delta
return numpy.float64(0.0)

其中 self 是误差类的 __call__ 函数，也就是用于计算给定魔法数字误差的函数。

依然使用之前的抽样间隔，得到的导数走势大致如下：

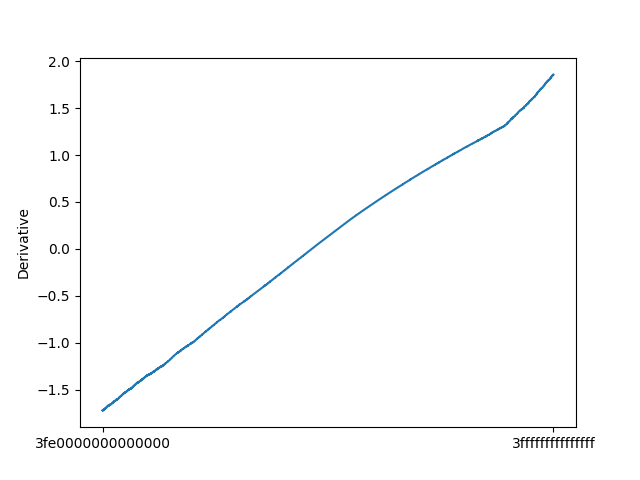
Derivative

之后就是梯度下降了，对于这样的一元函数，梯度值就是导数值，只要不断沿着负梯度方向，就可以不断减小误差函数的值；而训练的终止条件设置为导数值小于某一个给定的参数值即可：

epsilon, lr = 1e-5, 2**32
x = args.start
dx = ef.d(x)
while abs(dx) > epsilon:
    x -= int(dx * lr)
    dx = ef.d(x)

这里设置的导数临界值为 $10^{-5}$，学习速率设置为 $2^{32}$，之后开始训练：

......
iter 4424625: error 0.013024344518583695 at 3feed5866c3ea0a1, next -0.000519
iter 4440345: error 0.013024330119425524 at 3feed58dae6945ca, next -0.000543
iter 4455970: error 0.013024316601644746 at 3feed594b3a58ff8, next -0.000451

这是误差函数随训练轮数的走势：

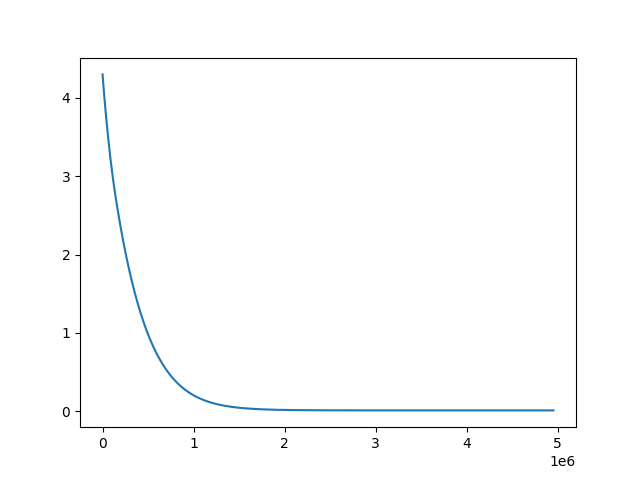
Training