用生成树算法解决商品生成问题

This article was last updated on <span id="expire-date"></span> days ago, the information described in the article may be outdated.

前几天项目写到了 spu、sku 部分，遇到一个需求：用户手动管理产品，需要根据给定的产品类目生成品类所有商品。

这么说大家可能不明白，给大家举一个例子吧：

假设用户添加了一个产品类目：Apple MacBook Pro 2018，这个产品有很多属性，譬如可以调整处理器、内存大小、硬盘大小…

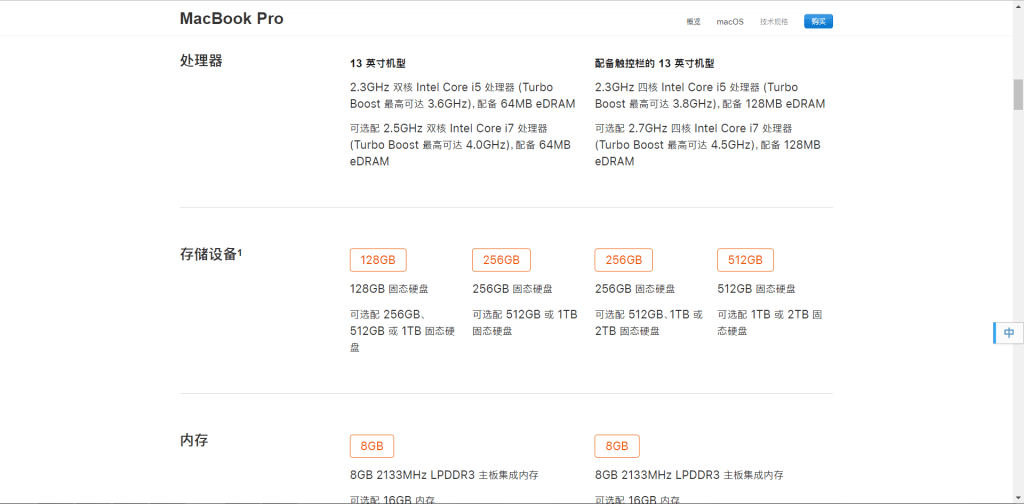
假设我们可以选择的部分写成一个字典，大概就是这样的：

selections = {
  "尺寸": ("13.3 英寸", "15 英寸"),
  "内存": ("8GB", "16GB", "32GB"),
  "硬盘": ("128GB", "256GB", "512GB", "1TB", "2TB"),
  "处理器": ("Intel Core 第八代 i5", "Intel Core 第八代 i7")
}

这样一来我们在数据库中一共就要生成 2*3*5*2 = 60 种不同的型号，他们大概长这个样子：

'skus': {
  ['13.3 英寸', '8GB', '128GB', 'Intel Core 第八代 i5'],
  ['13.3 英寸', '16GB', '128GB', 'Intel Core 第八代 i5'],
  ['13.3 英寸', '16GB', '256GB', 'Intel Core 第八代 i5'],
  ...
}

显然，让用户手动去一个个添加不现实，这样的系统也是没有人愿意用的，那么问题来了我们该如何根据提供的信息生成这些商品呢？

我在这里利用树的生成与遍历算法解决这个问题。

我们想象将每一个商品信息都添加为一棵树上的节点，那么我们可以得到大概这样的一颗树：

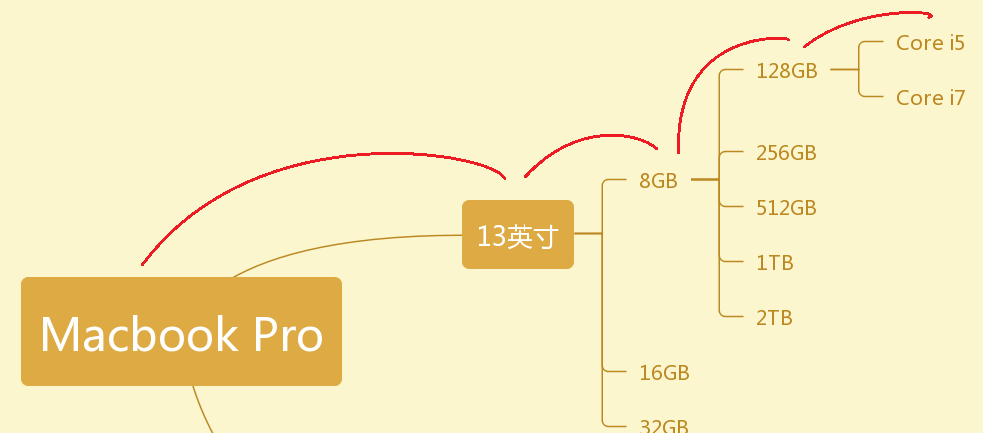
产品信息树

这里由于树分支太多，我只对后面两级的第一支做了分支。

可以看到，当我们生成这样一颗产品树之后只需要沿着路径对产品信息树进行遍历所有的叶子节点既可以生成所有的详细产品信息：

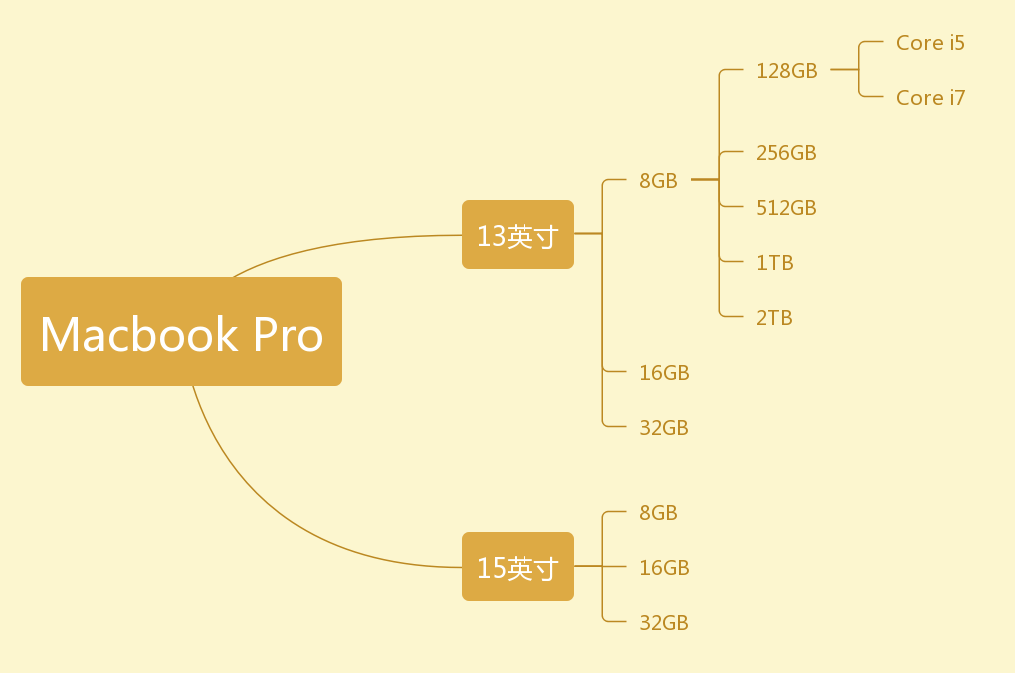
遍历树的第一个分支

我们这样就生成了第一条产品信息：

1	['13.3 英寸', '8GB', '128GB', 'Intel Core 第八代 i5']

生成树

下面我们来讨论如何使用给定的信息来生成这样一棵树。

我们首先定义一个节点类，类里面最好存储一下这个节点的度，方便我们后面遍历使用：

# Author: [email protected]
class Node(object):
    """树节点"""
    def __init__(self, value = None):
        self.__degree = 0
        self.value = value
        self.__children = list()

    def degree(self):
        return self.__degree

    def child(self):
        """返回最后一个子节点"""
        return self.__children[self.__degree - 1]

    def children(self, index = 0):
        """返回子节点迭代器"""
        while index < self.__degree:
            yield self.__children[index]
            index += 1

    def remove_child(self):
        """“删除”一个子节点"""
        self.__degree -= 1

    def add_child(self, node):
        self.__degree += 1
        self.__children.append(node)

    def add_children(self, *nodes):
        self.__degree += len(nodes)
        self.__children.extend(nodes)

这里的 remove_child 方法不对 self.__children 进行 pop 操作的原因会在底下进行解释（当然我猜大家也都知道啦~）

类中有一个 children 方法会返回子节点的迭代器，因为我们在其他任务中不一定需要完全子节点列表（例如搜索任务），只需要对子节点进行遍历即可，这样可以节省一定的内存，而不失优雅性。

接下来我们观察树的结构：

这是一颗多叉对称树
树的每一个同级分支都是相同的
树具有完全树的性质（即所有叶子节点同级）

由于第二条性质，我们考虑使用类似 BFS 的方法遍历生成树，这样在遍历过程中，在每一级中只需要取到该级别的信息，添加子节点即可。

由于是使用 BFS 方法生成树，我们需要一个队列（先进先出）来保存下来需要继续遍历节点的详细信息，我们这里使用 Python 自带的 queue

在这里我们不需要不断地查询节点需要使用哪一个级的数据，我们可以使用一个二元数组 tuple(level, node) 来直接保存需要继续遍历的节点与对应节点，而每次进入子节点遍历时，只需要将 level 值加一即可；而对从任务队列中取出的遍历任务，直接将 level 赋值成保存的值即可。

这样一来我们就可以写出代码：

def make_tree(details):
    """将传入的详细信息生成满多叉树"""
    root = Node(None)
    # 用 BFS 算法生成树
    index, height = 0, len(details)
    tasks = queue.Queue()
    tasks.put((root, index))

    while tasks.qsize():
        node, index = tasks.get()
        children = [Node(item) for item in details[index]]
        node.add_children(*children)
        index += 1
        if index == height:
            continue
        for task in node.children():
            tasks.put((task, index))
    return root

好了，我们已经构造好了这样一颗产品信息树。现在我们只需要对他进行遍历就可以获取详细的产品信息啦。

遍历树

在遍历树的过程中，我们关注的重点是当前节点是否是叶子节点，如果是的话则将路径与节点拼接返回即可。所以采用 DFS 进行遍历可能是一个更好的选择，因为这样我们可以方便的获取到叶子节点的路径。

一般情况下我们需要使用一个列表去保存整棵树我们已经访问过的节点防止进入死循环，但是当树的节点非常多时，我们就需要大量的内存来保存这个列表。

还有一个问题，就是每次我们判断节点是否在列表中时都需要 in 操作符，这个操作是 O(n) 的，也会比较耗费性能。

所以我在上面定义节点的时候加入了一个 remove_child 方法，既然我们生成信息之后这棵树就没有存在的必要了，那我们就通过剪枝的方法来防止遍历死循环。

细心的朋友可能会发现我在定义 remove_child 方法时候并没有将子节点从子节点列表中 pop 出去，而只是将该节点的度减一，这是为什么呢？

我们在定义类的时候，将 __children 设置为了私有属性，外部是无法访问的，而作为一个栈，它肯定是有序的，我们在两个对外部访问子节点的接口中都只是根据当前节点的 degree 去进行返回，所以我们没有必要对 children 列表进行 pop 操作，这样一来，在每次剪枝的时候就可以又少一步操作。

由于 Python 的垃圾回收会帮我们做内存回收，所以这里不用担心内存泄漏的问题（最近 C++ 作业写的魔障了…）

OK，经过上面的分析我们可以写出如下的代码了：

def traverse_tree(root, height, func):
    """遍历生成的树生成产品详细信息"""
    # 用 DFS 算法遍历树
    current = root
    result = list()

    path = list()
    while True:
        if current.degree() is 0:
            if len(path) == height:
                ####################################
                result.append(func(path, current))
                ####################################
            previous = current
            if not len(path): break
            current = path.pop()
            current.remove_child()
            continue
        child = current.child()
        path.append(current)
        current = child

    return result

这里第二个参数 height 是需要遍历的高度，我们要取得所有叶子节点，就传入一共有多少级信息（也就是树的高度）。

这里的第三个参数 func 是你想对路径和当前节点操作的函数，记得返回值。

我这里使用了这样的函数：

def splice(path, current):
    npath = [node.value for node in path]
    npath.remove(None)
    npath.append(current.value)
    return tuple(npath)

细心的朋友可能会发现，我这里对路径 remove 了 None，因为我们的根节点是没有 value 值的，所以所有 path 的第一个 value 值都是 None。其实完全没有必要这么做（在后期遍历的时候跳过第一个即可），但是为了结果的清楚，我这里使用了 remove 这个效率并不高的操作。

结果

我们运行上面的代码（使用 selections 作为测试数据），就可以得到这样的结果：

可以看到，生成了 60 条结果，结果还是蛮不错的O(∩_∩)O~~

这是我的测试用代码，供大家参考：

selections = {
  "尺寸": ("13.3 英寸", "15 英寸"),
  "内存": ("8GB", "16GB", "32GB"),
  "硬盘": ("128GB", "256GB", "512GB", "1TB", "2TB"),
  "处理器": ("Intel Core 第八代 i5", "Intel Core 第八代 i7")
}

details = list(selections.values())
tree = make_tree(details)
result = traverse_tree(tree, len(details), splice)
for i in result: print (i)

总结

整个算法经过测试在日常数据集生成过程中暂时没有很卡顿的情况出现，效率应该在 O(b^m) ，在我的项目中暂时够用了。

其实这个需求我也是头一次接触，5min 想到了用树去解决，我觉得一定有效率更好的解决方案，只是我现在不知道而已，如果有大佬知道可以在评论区评论哈！

才疏学浅，上面地方如有疏漏错误，还请大家指出哈！

Author: 桂小方

Permalink: https://init.blog/1616/

文章许可协议:

如果你觉得文章对你有帮助，可以支持我

tech # Python # Tree # 商品生成

用生成树算法解决商品生成问题

生成树

遍历树

结果

总结

Comments